Obsah Elektro číslo 12/2001

Modelování indukčního ohřevu kovových materiálů
a souvisejících technologických procesů

1. Úvod

Indukční ohřev kovových materiálů patří v současné době mezi velmi dobře propracované a zvládnuté technologie a je široce využíván v mnoha průmyslových odvětvích. Jako příklady lze uvést indukční kalení, popouštění, vysoušení povrchu znečištěných součástí, tavení kovů, lisování za tepla atd. Mezi jeho hlavní výhody patří:

• relativně snadné řízení intenzity ohřevu a rozložení teploty ve vsázce,
• absence chemických změn v povrchových vrstvách vsázky (na rozdíl od jiných způsobů ohřevu, např. plynem), jež mohou vést ke zhoršování fyzikálních vlastností ohřívaného materiálu,
• šetrnost k životnímu prostředí (odpadají problémy s produkty spalování, z nichž některé mohou být i toxické).

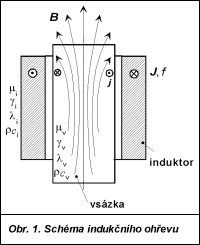
Princip indukčního ohřevu je jednoduchý a je schematicky znázorněn na obr. 1. Vsázka, která musí být dostatečně elektricky vodivá, se vloží do induktoru (zpravidla masivnější cívka) protékaného střídavým proudem o hustotě J a kmitočtu f. Ten vyvolá magnetické pole B procházející vsázkou, v níž se následně indukují vířivé proudy o hustotě j. Ty se uvnitř vsázky uzavírají a generují zde ztráty, jež se projevují zvýšením její teploty (průchodem budicího proudu se ovšem ohřívá i induktor). Hloubku prohřátí vsázky lze dobře regulovat kmitočtem; s rostoucím kmitočtem budicího proudu se ztráty, a tedy teplo, generují v tenčích a tenčích povrchových vrstvách.

Vzhledem k tomu, že indukční ohřev je proces zpravidla energeticky velmi náročný, je nezbytné celý systém (induktor, vsázku a další prvky) optimalizovat tak, aby při zadaných požadavcích na průběh procesu byla jeho účinnost co nejvyšší. Navíc je často zapotřebí dodržet určitý časový režim ohřevu, popř. jiné parametry (rozložení teplot apod.). V určitých (zejména jednodušších) případech je možné na základě předchozích zkušeností vypracovat korektní návrh systému splňujícího uvedené požadavky. Většinou se však tento návrh neobejde bez vyřešení přiměřeně přesného matematického modelu a bez optimalizace.

Článek shrnuje současný stav v oblasti matematického a počítačového modelování indukčního ohřevu a souvisejících fyzikálních procesů jako následné kalení, lisování za tepla apod., a prezentuje množství výsledků, k nimž autorský kolektiv dospěl v posledních letech v rámci řešení několika národních i mezinárodních projektů.

2. Modelování indukčního ohřevu

Indukční ohřev tuhých materiálů je popsán dvěma obecně nelineárními parciálními diferenciálními rovnicemi parabolického typu. První z nich popisuje rozložení elektromagnetického pole vybuzeného induktory (jež má prostorový charakter a navíc se může měnit s časem), druhá pole teplot, které je již zpravidla výrazně nestacionární. Roztaví-li se ohřívaný materiál, je nutné dalšími diferenciálními rovnicemi respektovat i pohyb taveniny. Řešení vzniklé soustavy rovnic je neobyčejně komplikované zejména proto, že jejich koeficienty, dané materiálovými vlastnostmi, jsou závislé na teplotě, a magnetická permeabilita (je-li přítomno feromagnetikum) i na velikosti magnetického pole. V některých případech se mohou objevit i další potíže se stanovením okrajových podmínek (elektromagnetické pole nemusí být ohraničené, v případě teplotního pole může být nesnadné stanovit koeficienty charakterizující konvekci tepla do okolního prostředí či sálání), s geometrickou nesouměřitelností (např. ohřev tenkých plechů), s měnícím se proudem v induktoru, ať už v důsledku zvyšující se rezistance (cívka se protékajícím proudem ohřívá) či poklesu reaktance celého obvodu (permeabilita feromagnetické vsázky se s rostoucí teplotou zmenšuje), s pohybem vsázky či induktoru atd. Často je úloha prostorově tak rozsáhlá, že kapacita běžných počítačů k jejímu vyřešení nestačí nebo doba potřebná k jejímu vyřešení je neúnosně dlouhá.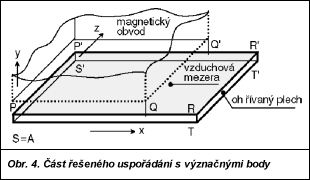

Přístupy k formulacím matematického modelu jsou v zásadě dva: slabě sdružený a kvazi (přibližně) sdružený. Oba budou ilustrovány na indukčním ohřevu tuhé vsázky.

2.1 Slabě sdružená formulace
Nejprve se v daném uspořádání vyřeší rozložení elektromagnetického pole, a to s materiálovými vlastnostmi odpovídajícími střední teplotě v dané soustavě. Z něho se určí rozložení měrných ztrát ve vsázce, jež se pokládá v čase za konstantní. S tímto rozložením zdrojů tepla se poté řeší rovnice popisující nestacionární teplotní pole, a to buď až do ustáleného stavu, nebo do požadovaného rozložení teplot.

Nespornou výhodou této formulace je skutečnost, že se vždy řeší pouze jedna rovnice. To vede k velmi výrazné úspoře doby potřebné ke zvládnutí výpočtu, naproti tomu ovšem může nastat situace, že výsledky jsou zatíženy chybou o nepřípustné velikosti. Jako příklad lze uvést ohřev feromagnetické vsázky na kalicí teplotu, která se pohybuje v okolí Curieova bodu ^*). Bude-li v tomto případě uvažována relativní permeabilita vsázky konstantní o velikosti stovek či tisíců (což bývá obvyklé), na konci procesu, kdy ve skutečnosti její hodnota poklesne k jedné, budou výsledky velmi zkreslené a často nepoužitelné.

2.2 Kvazi sdružená formulace
Řešení probíhá v iteračním (opakovaném) cyklu, jenž může být popsán těmito body:

a) Výpočet elektromagnetického pole při materiálových parametrech (elektrická vodivost g a magnetická permeabilita µ) odpovídajících počáteční teplotě systému a stanovení rozložení měrných ztrát ve vsázce.

b) Výpočet nestacionárního teplotního pole ve vsázce až do okamžiku, kdy její střední teplota (nebo teplota v určitém místě) vzroste o předepsanou hodnotu DT.

c) Korekce materiálových parametrů na aktuální teplotu a nový výpočet elektromagnetického pole pro tyto parametry.

d) Návrat do bodu b) a opakování bodů b) a c) až do okamžiku, kdy je výpočet dokončen (dosáhlo se požadovaného rozložení teploty).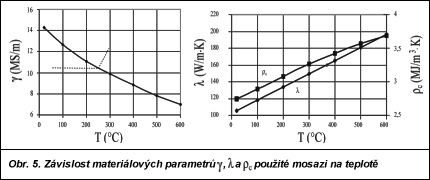

Je zřejmé, že obdržené výsledky jsou daleko přesnější a se snižováním hodnoty DT se neustále zpřesňují, ovšem na úkor doby výpočtu. V limitním případě (DT®0) lze hovořit o silně sdružené formulaci, jejíž realizace je schůdná jen ve velmi jednoduchých případech.

Vždy je třeba mít na paměti, že elektromagnetické pole je nutné určovat zpravidla v mnohem větší oblasti než pole teplot (jeho znalost je potřebná jen v ohřívaném tělese, popř. induktoru). Proto jeho řešení klade daleko vyšší nároky na paměť i čas použitého počítače než řešení teplotního pole, a příslušným algoritmům a metodám je tedy nutné věnovat daleko větší pozornost.

V současné době existuje několik profesionálních programů, které jsou založeny na slabých či jednodušších kvazi sdružených formulacích a metodě konečných prvků, jež umožňují modelovat určité (zdaleka ne však obecné) spektrum úloh. Ze známějších lze uvést např. Flux, Ansys a Sysweld. Tyto programy jsou ovšem velmi nákladné (jejich cena se pohybuje na úrovni mnoha set tisíc korun). Schůdnou cestou pro řešení specifických úloh se proto jeví využití levnějších programů (specializovaných např. na řešení elektromagnetického pole) doplněných vlastními uživatelskými procedurami pro mapování následných jevů. V dalším textu bude jejich využití demonstrováno na několika ilustrativních příkladech.

3. Ilustrativní příklady

Na Slezské technické univerzitě v Katovicích byl zkonstruován induktor na indukční ohřev tenkých plechů, jenž slouží zejména k experimentálnímu ověřování teoreticky získávaných výsledků. Jeho uspořádání je schematicky znázorněno na obr. 2.

Během provozu vzniká v prostoru vzduchové mezery příčné magnetické pole (díky přítomnosti magnetického obvodu nemá harmonický, ale pouze periodický charakter) a v rovině plechu indukuje vířivé proudy potřebné k jejímu ohřevu. Plech se během ohřevu navíc může pohybovat ve vyznačeném směru rychlostí v.

Jeden z prvních souborů výpočtů se týkal optimalizace tvaru induktoru a jeho cílem byl návrh takové jeho geometrie, která by zajistila nejvýhodnější rozložení Jouleových ztrát (a tedy zdrojů tepla) v ohřívaném materiálu, a to při dané šířce induktoru, vzduchové mezeře a počtu závitů budicích cívek. V úvahu připadala dvě uspořádání; poloviny jejich osových řezů, včetně směrů proudů v závitech, jsou znázorněny na obr. 3.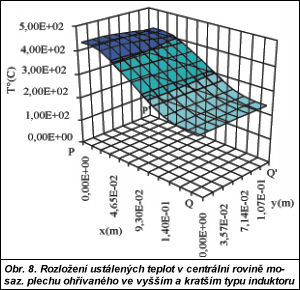

Základní rozměry induktoru jsou zřejmé z obr. 3. Jeho celková šířka (ve směru osy z kolmé k nákresně) je 0,25 m, vzduchová mezera má šířku 0,01 m nebo 0,02 m, což je zcela postačující pro manipulaci s plechem. Závity budicího vinutí jsou duté, protékané chladicím médiem (vodou) a jsou zapojeny v souladu s naznačenými šipkami.

Vzhledem k tomu, že obě uspořádání mají výrazný 3D (threedimensional – trojrozměrný) charakter, byla jejich analýza velmi komplikovaná. Pro mapování elektromagnetického pole byl použit program Opera (modul Elektra pro analýzu harmonických polí) a pro vyhodnocení nestacionárního teplotního pole soubor programů vyvinutých autory. Ohřívaný plech (obr. 4) byl hliníkový, mosazný, měděný či želený a jeho tloušťka se měnila v rozmezí 0,002 až 0,0032 m. V širokých mezích se měnila i amplituda budicího proudu a kmitočet.

Pro ilustraci je uvedeno několik výsledků získaných při výpočtech ohřevu mosazné desky o tloušťce 0,0032 m (závislost materiálových vlastností mosazi na teplotě je vidět na obr. 5).

Na obr. 6 je ukázáno rozložení Jouleových ztrát w_J v této desce při budicím proudu I = 500 A o kmitočtu f = 50 Hz, má-li induktor tvar znázorněný v pravé části obr. 3, šířka vzduchové mezery je 0,01 m a střední teplota desky je 200 °C. Podobně obr. 7 zobrazuje totéž rozložení, má-li induktor tvar uvedený v levé části obr. 3.

Podobných výpočtů bylo uskutečněno několik set. V souladu s experimenty se ukázalo, že nezávisle na materiálu vsázky je hustota Jouleových ztrát vždy vyšší v případě vyššího a kratšího induktoru (na obr. 3 vpravo). S rostoucím kmitočtem budicího proudu narůstá nerovnoměrnost rozložení specifických ztrát w_J; nejvyšších hodnot této veličiny je dosaženo podél podélné vnější hrany plechu, kde vířivé proudy mění svůj směr. Dále se ukazuje, že vyšší elektrická vodivost vsázky má za následek nižší střední Jouleovy ztráty.

Nestacionární tepelné výpočty realizované ve zmíněné kvazi sdružené formulaci řešil vlastní program, a to jen pro výhodnější tvar induktoru (obr. 3 vpravo). Obr. 8, navazující na obr. 6, znázorňuje ustálené rozložení teploty (dosaženo po asi 20 min ohřevu). Na obr. 9 je ukázán časový průběh teploty ve vybraných bodech desky od počátku ohřevu do ustáleného stavu.

Závažným problémem výpočtu byla diskretizace^**) vyšetřované 3D oblasti pro elektromagnetický výpočet. Potíže byly způsobeny skutečností, že ohřívaný materiál je oproti dalším prvkům v systému dosti tenký a při použití metody konečných prvků (na níž je program Opera založen) obsahuje výsledná síť prvky o velmi se lišících rozměrech. Je známo, že výpočty na takových sítích mohou vést ke značným numerickým chybám. Navíc v daném případě byl počet těchto prvků dosti malý (asi 25 000 – více použitá verze programu Opera v systému Windows neumožňuje), a výsledné elektromagnetické pole tudíž bylo modelováno spíše hrubě. Zpracování jedné varianty na PC 800 MHz trvá asi 1 h.

Po rozhodnutí prozkoumat, zda by v případě modelování indukčního ohřevu tenkých desek nebylo možné použít jiný přístup, než jaký poskytuje metoda konečných prvků či jiné diferenciální metody, byl zjištěn výsledek, že v lineárním prostředí bez přítomnosti feromagnetických částí lze využít integrální přístup. Jeho výhoda spočívá v tom, že pomocí vhodné integrální rovnice lze přímo stanovit rozložení hustot vířivých proudů v desce a nemusí se vůbec řešit rozlehlé elektromagnetické pole. Naproti tomu má tato metoda určitou nevýhodu. Na rozdíl od metod diferenciálních, kde hodnota hledané veličiny pole v uzlu závisí pouze na hodnotách v sousedních uzlech, v případě integrálních metod závisí na hodnotách ve všech uzlech sítě. Jinými slovy, diferenciální přístup vede k výpočtům na daleko rozsáhlejších sítích, ale matice soustavy je řídká, zatímco integrální přístup vede k matici mnohem menší, ale plně obsazené. Avšak jelikož lze desku či tenký plech diskretizovat velmi rovnoměrně, není problém (z hlediska algoritmizace) napsat vlastní program. Rovněž program pro teplotní výpočty, byť i ve 3D, není po stránce algoritmů příliš složitý.

Na tomto základě byl sestaven program pro mapování indukčního ohřevu tenkých i silných nemagnetických desek, hranolů a podobných těles ohřívaných induktory libovolných tvarů, ovšem bez magnetického obvodu. Ohřívané těleso se může pohybovat, stejně jako kterýkoliv induktor; pohyb je popsán parametricky. Program respektuje vliv teploty na materiálové parametry a celkovou formulaci problému lze pokládat za téměř silně sdruženou.

Následující příklad ilustruje použití této metody. Mosazná deska o rozměrech podle obr. 10 byla z jedné strany ohřívána induktorem ve tvaru cívky o dvaceti závitech bez železného jádra, jíž protékal proud I = 8 500 A o kmitočtu f = 2 kHz. Žádná z částí uspořádání se nepohybuje. Počáteční teplota celého systému je 20 °C, konvekce tepla z ohřívané desky do vzduchu je charakterizována součinitelem a = 25 W/m²·K.

Obr. 11 znázorňuje rozložení teploty podél horního povrchu desky po 60 s ohřevu. Spodní vrstvy desky (vzdálenější od induktoru) jsou ohřívány pomaleji, ale vlivem dobré tepelné vodivosti mosazi nepřesahují rozdíly nejteplejších míst na horním a spodním povrchu desky asi 20 °C.

Nakonec obr. 12 znázorňuje časový průběh teploty „nejteplejšího“ bodu desky H z obr. 10.

4. Závěr

Článek přináší informace o matematickém a počítačovém modelování indukčního ohřevu. V dalším článku (v některém z příštích čísel ELEKTRO) bude přiblíženo využití indukčního ohřevu při složitějších technologických postupech. Bude zde analyzována problematika následného kalení (včetně jeho počítačového modelu) a lisování osově symetrických spojů za tepla. Analýza bude opět doplněna ilustrativními příklady, z nichž některé byly experimentálně ověřeny.

Příspěvek byl zpracován na základě některých výsledků řešení projektu Výkonové a řídicí systémy elektromechanických přeměn energie MSM 232200008.

Ústav pro elektrotechniku AV ČR
Dolejškova 5
182 02 Praha 8
tel.: 02/86 58 30 69
fax: 02/86 89 04 33
e-mail: dolezel@iee.cas.cz

^*) Pozn. red.: Courieův bod (bod magnetické přeměny) – teplota, při níž zaniká feromagnetismus látek; při této teplotě tepelný pohyb atomů překoná vnitřní síly působící spontánní magnetizaci a látky se stávají paramagnetické; teplota Courieova bodu je např. u železa 769 °C, niklu 358 °C, kobaltu 1 115 °C atd.

^**) Diskretizace je náhrada spojitého prostředí soustavou diskrétních bodů, ve kterých se soustředí fyzikální parametry příslušného místa prostředí.